フレッツ 光ネクストのインターネットが頻繁に切れるので、 ひかり電話対応機器 PR-400MI 回線切れる 時の対処法 をまとめてみました。
目次
IPv4(PPPoE) IPv4 over IPv6(IPoE)
接続が IPv4(PPPoE) か IPv4 over IPv6(IPoE) で設定が変わります。
PPPoE と IPoE の 違い
PPPoE と IPoE の 違い

PPPoE と IPoE の 違い IPv4 over IPv6 とは PPPoE と IPoE の 違い PPPoEIPoEIDとパスワードによる認証必要不要…
jikuu.site
IPv4(PPPoE)
PR-400MIのルータ機能、使わないことにしました。
PR-400MI のインターネット接続を未設定にして、無線LAN ルーター でインターネット設定をしました。

PR-400MI の ルーター 機能 使わないことにしました。 PR-400MI のインターネット接続を未設定にして、無線LAN ルーター でインターネット設定…
jikuu.site
ひかり電話対応機器 PR-400MI 回線切れる 時の対処法
PR-400MI のインターネット接続を未設定にして、無線LAN ルーター でインターネット設定しています。
リンク
ACTIVEボタンで判断
ACTIVEボタンが 緑点灯でインターネットに接続できない時は、パソコン側の問題
ACTIVEボタンが緑点滅すると、「ひかり電話ルーター」に問題
無線LANルーターに問題がないので「診断」で済ませました。
無線LANルーターにルーター機能を任せ ているのでACTIVEボタンが緑点滅すると、「ひかり電話ルーター」に問題があるので「ひかり電話ルーター」の電源を入れなおすタイミングだと分かるようになりました。
無線LANルーター にルーター機能を任せているのでACTIVEボタンが緑点滅すると、「ひかり電話ルーター」に問題があるので「ひかり電話ルーター」の電源を入れなお…
jikuu.site
ひかり電話対応機器 PR-400MI 久しぶりに回線切れました。
有線・無線LANホームルーターである「AtermWG300HP PA-WG300HP」のACTIVEボタンが久しぶりに点滅していました。

ひかり電話対応機器 PR-400MI 久しぶりに回線切れました。 無線LANルーターのACTIVEボタンが久しぶりに点滅していました。 2014年1月10日の記…
jikuu.site
IPv4 over IPv6(IPoE)
PR-400MI IPv4 over IPv6 設定 変更
ASAHIネット IPv4 over IPv6 が 光回線速度測定 で 70Mbps 前後しか出なくなったので PR-400MI IPv4 over IPv6 の 設定 を 変更 しました。
ASAHIネット IPv4 over IPv6 が 光回線速度測定 で 70Mbps 前後しか出なくなったので PR-400MI IPv4 over IPv6 …
jikuu.site
AsahiNet光 IPv4 over IPv6 遅い ときの 確認
AsahiNet光 IPv4 over IPv6 遅い ときは ひかり電話ルーター の PPPランプを 確認 します。

AsahiNet光 IPv4 over IPv6 遅い ときは ひかり電話ルーター の PPPランプを 確認 します。 ひかり電話ルーター の PPPランプ を…
jikuu.site
IPv4overIPv6 対応 プロバイダ
IPv4overIPv6 対応 プロバイダ
IPv6環境で通信を行いながら、IPv4アドレスでの通信も可能にする技術

IPv4overIPv6 対応 プロバイダ IPv4 over IPv6 とは IPv6ネットワークの入口で IPv4パケットをIPv6パケット内にカプセル化 …
jikuu.site
家庭内LAN(ホームネットワーク)の構築方法
- PR-400MI 回線切れる 時の対処法
- ipv4 over ipv6接続 の AsahiNet 光 に 転用しました
- パソコンの動画をDIGA(ディーガ)で再生する。
- DIGA の USER_area が パソコンに表示されない
- Ubuntu 18.04 LTSでサーバー構築ブログ
- 3種類のサーバー を使っています
- Eclipse Pleiades All in One PHP でホームページ作成
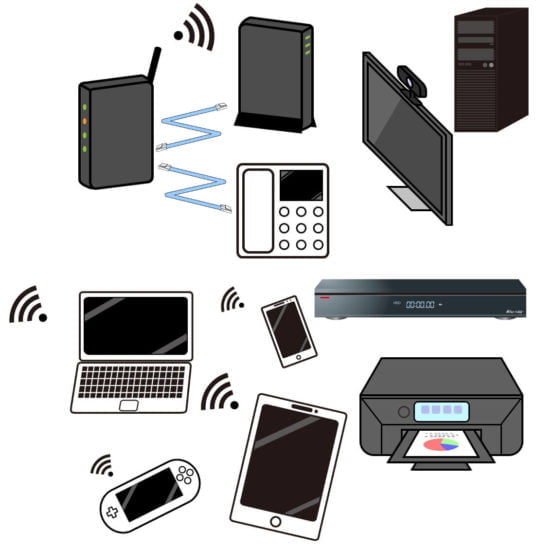
無線LANルーターを導入することで 家庭内LAN (ホームネットワーク)の 構築 は簡単にできます。 無線LANルーターの導入で 家庭内LAN(ホームネットワー…
jikuu.site
