家庭内LANの構築、家電の設置・修理、自動計算、テレビ 動画等 自分で出来ること を増やそうと思います。
オールラウンダー を目指したいと思います。

- 家庭内LANの構築方法
- 自分で 家電 を設置・接続・修理
- NHK の 英語テレビ講座 で英語を勉強する方法
- 大人 の 勉強 やり直し まとめ
- 腰痛 膝痛 新型コロナ 自動車等の 生活情報
- 自動計算
- テレビ 動画
- 身の丈DIY
- 畑で 家庭菜園 を初めて困ったトラブル事例と 対処法
- 独学 で 大学数学 を勉強する 順番
目次
家庭内LAN ( ホームネットワーク )の構築方法
無線LANルーターを導入することで 家庭内LAN ( ホームネットワーク )の構築は簡単にできます。
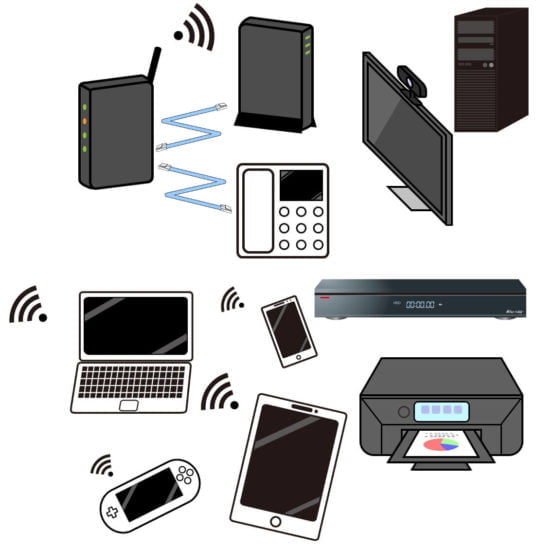
無線LANルーターを導入することで 家庭内LAN (ホームネットワーク)の 構築 は簡単にできます。 無線LANルーターの導入で 家庭内LAN(ホームネットワー…
jikuu.site
自分で 家電 を設置・接続・修理
家電 は 自分で 設置・接続・修理する方ですか?
実は、僕も家電は自分で設置・接続したい方です。
自分が今までにやってきた家電の設置・接続・修理をまとめてみました。

家電 は 自分で 設置・接続・修理 する方ですか? 実は、僕も家電は自分で設置・接続したい方です。 自分が今までにやってきた 家電の設置・接続・修理 をまとめて…
jikuu.site
NHK の 英語テレビ講座 で英語を勉強する方法
僕も NHK の 英語テレビ講座 でしか勉強はしたことがありませんが外国人とちょっとした会話ならできました。
英語を話せたり・聞き取れたり・読めるようにないりたいと思いませんか?

英語を話せたり・聞き取れたり・読めるようにないりたいと思いませんか?僕も NHK の 英語テレビ講座 でしか勉強 はしたことがありませんが外国人とちょっとした会…
jikuu.site
大人 の 勉強 やり直し まとめ
大人 の 勉強 の やり直し を まとめ てみました。
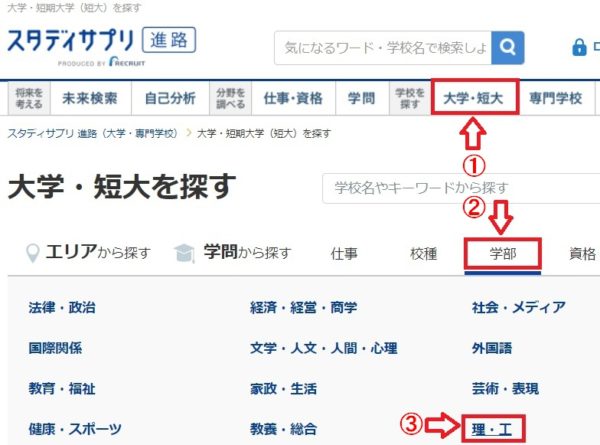
大人 の 勉強 の やり直し を まとめ てみました。 スタディサプリ進路 社会人向け の 使い方 スタディサプリ進路 社会人向け の 使い方 NHK の 英語…
jikuu.site
腰痛 膝痛 新型コロナ 自動車などの 生活情報
腰痛 膝痛 新型コロナ 自動車 自動計算ツールなどの 生活情報 を載せています。

腰痛 膝痛 新型コロナ 自動車等の生活情報 を載せています。 腰痛 膝痛 自動車等の生活情報 シャンプー 腰痛 膝痛 などの健康の知識 自動車 を 所有 してい…
jikuu.site
自動計算
自動計算ツール を揃えた自動計算サイト
農薬の希釈 自動計算ツール 西暦から元号変換ツール・コンクリート何m3からセメント何袋必要かを計算するツールあったらいいと思いませんか?
それらの 自動計算ツール を一つにまとめたのがこのサイトです。
農薬の希釈 自動計算ツール 西暦から元号変換ツール・コンクリート何m3からセメント何袋必要かを計算するツールあったらいいと思いませんか? それらの 自動計算ツー…
jikuu.site
テレビ 動画
テレビ を見る方法
テレビ を見る方法
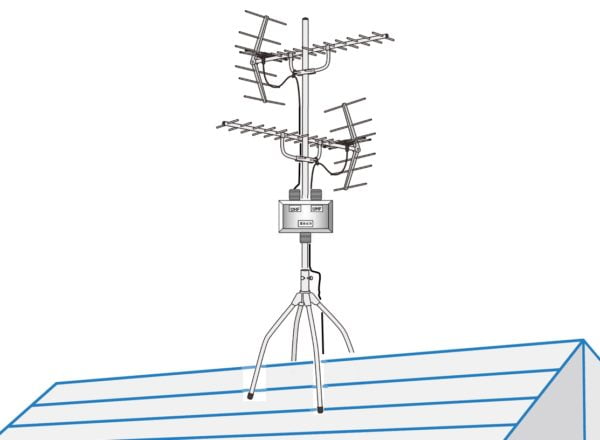
テレビ を見る方法 UHFアンテナ BS/110度CSアンテナ ケーブルテレビ NHKのBSメッセージの消去手続 スマホ で テレビを見る方法 動画配信サービス…
jikuu.site
身の丈DIY
自分の能力を把握し、出来る範囲のDIYを行います。

お金のかかる エクステリアDIY 自分でやりたいのが心情。自分がやってきたエクステリアDIYをまとめてみました。五十鈴エクステリアの物置の鍵を取り替えました。五…
jikuu.xyz
畑で 家庭菜園 を始めて困ったトラブル事例と 対処法
畑で 家庭菜園を始めて困ったトラブル事例とその 対処法を紹介します。

畑での 家庭菜園 では、野菜はさまざまな病気や害虫の被害に遭います。実際に体験した野菜の病気と害虫の被害とその 対処法 を紹介します。気軽に始められる家庭菜園で…
jikuu.xyz
独学 で 大学数学 を勉強する 順番
独学 で 大学数学 を学ぶ場合、 順番 に迷いますよね。
独学で放送大学の数学のテキストをほぼ読み終えた経験から順番を示したいと思います。

独学 で 大学数学 を学ぶ場合、 順番 に迷いますよね。独学で放送大学の数学のテキストをほぼ読み終えた経験から順番を示したいと思います。微分積分・入門線形代数は…
jikuu.work